ゲーム理論新版が難しすぎたので、ゲーム理論・入門新版--人間社会の理解のために (有斐閣アルマ) から読むことにした。

作者:岡田章
出版社/メーカー: 有斐閣
発売日: 2014/09/18
メディア: 単行本（ソフトカバー）

この章では、「実現可能集合」と「交渉の不一致点」によって「交渉」というものを定式化した上で、交渉解の求め方を説明する。

交渉の定式化
交渉解の求め方
- 公理論的アプローチ
- 戦略的アプローチ

交渉の定式化

交渉は「実現可能集合」と「交渉の不一致点」によってゲーム理論で扱える形に定式化することができる。

実現可能集合とは、交渉ゲームのプレイヤーが実現可能な利得ベクトルの全体である。

例えば、AとBが想定収益100万円の共同事業を始めようとしている場合、実現可能集合 $U$ は、 $u_A + u_B \leq 100, \: u_A \geq 0, \: u_B \geq 0$ である利得分配 $u = (u_A, u_B)$ の全体である。

交渉の不一致点とは、交渉が決裂したときのプレイヤーの利得ベクトルである。

例えば、上の共同事業の例において、交渉が決裂した場合、Aは単独でも50万円の収益を、Bは単独でも20万円の収益を上げることができるとした場合、交渉の不一致点 $d = (50, 20)$ である。

この様に、交渉問題は実現可能集合と不一致点の組 $(U, \: d)$ で表される。

また、不一致点 $d$ よりも大きい利得を得ないと協力する意味がないので、実現可能集合 $U$ に含まれ、かつ、不一致点 $d$ よりも大きい部分が、交渉の着地点として意味のある領域となる。これを交渉領域という。

上の共同事業の例で言うと、 $u_A + u_B \leq 100$ 、 $u_A > 50$ 、 $u_B > 20$ の三角形に囲まれた部分が交渉領域となる。

交渉解の求め方

定式化した交渉ゲームにおいて、プレイヤーが合理的であるならば実現するであろう合意を交渉解という。厳密に言うと、交渉解 $F$ とは、交渉問題 $(U, d)$ に対して合意される実現可能な利得ベクトル $F(U, d) \in U$ を対応させる関数である。

交渉解の求め方には、公理論的アプローチと戦略的アプローチとがある。

公理論的アプローチ

交渉解が満たすべき性質を公理として定式化し、それらの公理から交渉解を数学的に演繹する方法。

公理

交渉問題 $(U, d)$ の解を $F(U, d) \in U$ とおく。また、 $F_i (U, d) \in U$ を交渉解におけるプレイヤー $i \: (= 1, 2)$ の利得を表すものとする。交渉解の公理は下記の４つである。

公理 9.1 (強) パレート最適性

全ての $i = 1, 2$ に対して $t_i \geq F_i (U, d)$ で、少なくとも 1 つの $i$ に対して、 $t_i \gt F_i (U, d)$ である実現可能集合 $U$ の点 $t = (t_1, t_2)$ は存在しない。

要するに、交渉解はプレイヤーの利得を実現可能集合の範囲で最大化するということ。

公理 9.2 対称性

交渉問題 $(U, d)$ において、実現可能集合 $U$ が直線 $y = x$ に関して対称で $d_1 = d_2$ ならば、 $F_1 (U, d) = F_2 (U, d)$ である。

要するに、実現可能集合と交渉の不一致点が $y = x$ に対して対称なら、交渉解も $y = x$ に対して対称である、つまり利得はプレイヤー間で等しく分配されるということ。

公理 9.3 効用の正 1 次変換からの独立性

2 つの交渉問題 $(U, d)$ と $(U', d')$ の解をそれぞれ $F (U, d)$ と $F (U', d')$ とする。いま、プレイヤー $i \: (= 1, 2)$ の効用の正 1 次変換式 $u'_i = \alpha_i u_i + \beta_i, \: \alpha_i \gt 0$ に対して、
(1) 実現可能集合 $U$ が正 1 次変換式によって実現可能集合 $U'$ に移される。
(2) 不一致点 $d$ が正 1 次変換式によって不一致点 $d'$ に移される。
ならば、 $F_i (U', d') = \alpha_i F_i (U, d) + \beta_i, \: i = 1, 2$ が成り立つ。

公理 9.4 無関係な結果からの独立性

2 つの交渉問題 $(U, d)$ と $(T, d)$ において $U \subset T$ とする。もし $F (T, d) \in U$ ならば、 $F (U, d) = F (T, d)$ である。

要するに、実現可能集合が拡大された交渉問題の解 $F (T, d)$ が元の交渉問題でも実現可能であれば、それは元の交渉問題の解でもあるということ。

公理 9.1 〜 9.3 を使って交渉解を求める例

上の共同事業の例で言うと、 $u_A + u_B \leq 100$ 、 $u_A > 50$ 、 $u_B > 20$ の三角形に囲まれた部分が交渉領域となる。

このままでは「公理 9.2 対称性」を適用できないので「公理 9.3 効用の正 1 次変換からの独立性」を使って正 1 次変換式 $u'_A = u_A - 50, \: u'_B = u_B - 20$ によって、不一致点 $d = (50, 20)$ を $d' = (0, 0)$ に変換する。

この変換によって、実現可能集合 $U$ は新しい実現可能集合 $U'$ に変化する。ここで $U'$ は、 $u'_A + u'_B \leq 30$ を満たす利得分配 $u' = (u'_A, u'_B)$ の集合である。

新しい交渉問題 $(U', d' = (0, 0))$ に公理 9.1 と公理 9.2 を適用して、交渉解 $u' = (15, 15)$ を得る。これを再度「公理 9.3 効用の正 1 次変換からの独立性」を使って元の交渉問題 $(U, d)$ に戻して、交渉解 $u = (65, 35)$ を得る。

公理 9.1 〜 9.4 を使って交渉解を求める例

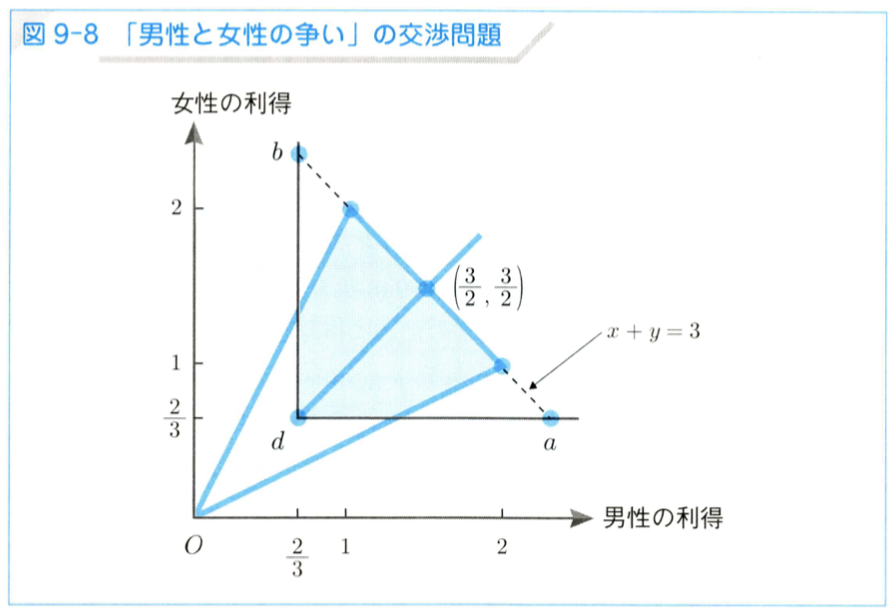
男女の争いゲームで、男女が話し合いをして野球に行くかバレエに行くかを決める状況を考える。

実現可能領域 $U$ は点 (0, 0), (1, 2), (2, 1) の三点に囲まれた領域であり、交渉の不一致点は混合戦略によるナッシュ均衡点 $d = (\frac{2}{3}, \frac{2}{3})$ とする。

公理 9.1 〜 9.3 だけでは解けないので、公理 9.4 を使うため、 $U$ を拡張した実現可能集合 $T$ として、x軸、y軸、直線 $x + y = 3$ に囲まれた領域を考える。

この時、交渉問題 $(T, d)$ の解は、利得ベクトル $(\frac{3}{2}, \frac{3}{2})$ である。

これは元の実現可能集合 $U$ に含まれるから、公理 9.4 より、交渉問題 $(U, d)$ の解は、利得ベクトル $(\frac{3}{2}, \frac{3}{2})$ である。

この交渉解は、男性と女性が等しい確率で (野球, 野球) と (バレエ, バレエ) の行動の組を選択する相関戦略を意味している。

f:id:mas178:20200107054803p:plain

ナッシュ交渉解

公理 9.1 〜 9.4 から下記の定理が導かれる。

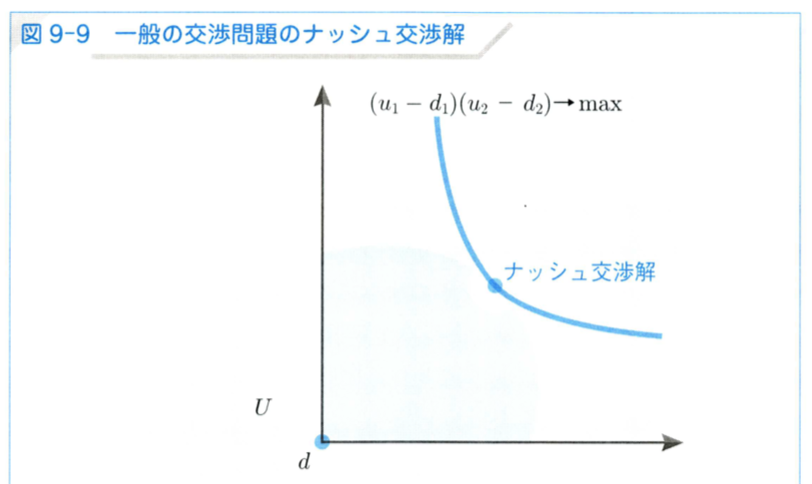
定理 9.1 ナッシュ交渉解

交渉問題 $(U, d)$ において、実現可能集合 $U$ は 2 次元平面の有閉界な凸集合で、 $u_i \gt d_i, \: (i = 1, 2)$ を満たす $U$ の点 $u = (u_1, u_2)$ が存在するとする。この時、公理 9.1 〜 9.4 を満たす交渉解 $F$ がただ一つ存在し、交渉解 $F$ は、全ての交渉問題 $(U, d)$ に対して、 $(u_1 - d_1)(u_2 - d_2)$ を最大にする利得ベクトル $F (U, d) = (u^*_1, u^*_2) \in U$ を対応させる関数である。

この解をナッシュ交渉解という。ナッシュ交渉解はプレイヤーの効用差の積 $(u_1 - d_1)(u_2 - d_2)$ を最大にするものである。この積をナッシュ積という。

f:id:mas178:20200107060313p:plain

戦略的アプローチ

合意にいたる交渉のプロセスを戦略形ゲームまたは展開形ゲームとして定式化し、ゲームのナッシュ均衡点として交渉解を求める方法。

再び共同事業の例で説明する。改めて状況をまとめる。

AとBが想定収益100万円の共同事業を始めようとしている中で、事前に収益の分け方を交渉によって決めようとしている。
交渉が決裂した場合は、双方の収益は0万円となる。
つまり、交渉問題 $(U, d)$ 、 $u_A + u_B \leq 100, \: u_A \geq 0, \: u_B \geq 0$ 、利得分配 $u = (u_A, u_B) \in U$ 、交渉の不一致点 $d = (0, 0)$ である。

これを下記の様なダイナミックなゲームとして定式化する。これは交互提案ゲームと呼ばれる、ルービンシュタインによって定式化された交渉ゲームである。

最初のラウンドで、プレイヤー 1 が分配 $(x_{11}, 100 - x_{11})$ を提案する。 $x_{it}$ は、 $t$ ラウンドに提案されたプレイヤー $i$ の取り分を表す。
次にプレイヤー 2 がその提案を受け入れるかどうかを決定する。もし、プレイヤー 2 が提案を受け入れれば、ゲームは終了し提案が合意される。もし、プレイヤー 2 が提案を拒否すれば、提案者を交代して次のラウンドに進む。
交渉は $n$ 回のラウンドまで行われる。 $t$ 回目のラウンドで分配 $(x_{1t}, x_{2t})$ が合意される時、プレイヤー $i$ の利得は、 $\delta^{t - 1} x_{it}$ である。( $\delta$ は将来利得に対する割引因子 )
合意が成立しない場合、プレイヤーの利得は $0$ である。

交互提案ゲームの部分ゲーム完全均衡点を求める。

交渉回数を回、応答者が初回に受け入れ可能な利得の最小値をとおくと、
- $z_1 = 0$
- $z_2 = 100 \: \delta$
- $z_n = \delta \: (100 - z_{n - 1})$
を限りなく大きくすると、
- 極限値 $z^* = \delta \: (100 - z^*)$ となり、
- これを $z^*$ について解くと、 $z^* = \frac{100 \delta}{1 + \delta}$ となり、
- 部分ゲーム完全均衡店の利得分配は $(\frac{100}{1 + \delta}, \frac{100 \delta}{1 + \delta})$ に収束する。
将来利得の割引因子 $\delta$ が限りなく $1$ に近くなると、利得分配は $(50, 50)$ に収束する。