読書メモ

個人的な読書メモ。それ以上でも以下でもありません。

ゲーム理論・入門 新版 (岡田章) 第08章 不確実な相手とのゲーム

ゲーム理論 経済学

ゲーム理論 新版 が難しすぎたので、ゲーム理論・入門 新版--人間社会の理解のために (有斐閣アルマ) から読むことにした。

ゲーム理論・入門 新版--人間社会の理解のために (有斐閣アルマ)

ゲーム理論・入門 新版--人間社会の理解のために (有斐閣アルマ)

  • 作者:岡田 章
  • 出版社/メーカー: 有斐閣
  • 発売日: 2014/09/18
  • メディア: 単行本（ソフトカバー）

この章では、プレイヤーの選好を表す利得関数や、ゲームのルールが不確実な状況におけるゲームについて説明する。

1. 基本概念

まずは基本概念を整理する。

  • 情報完備ゲーム (game with complete information): プレイヤーの利得関数や戦略集合を規定するゲームのルールがゲームに参加する全てのプレイヤーの共有知識であるゲーム。
  • 情報不完備ゲーム (game with incomplete information): プレイヤーが利得関数やルールについて不完全な情報しか持たないゲーム。
  • 個人情報 (private information): 特定の個人しか知らない情報。例えば、Aは野球が好きで、Bはバレエが好きなど。
  • タイプ (type): プレイヤーの個人情報の総称。例えば、Aは野球好きなタイプで、Bはバレエが好きなタイプなど。
  • 公的情報 (common knowledge): 全プレイヤーが知っている情報。
  • 非対称情報ゲーム (game with asymmetric information): 個人情報が存在するゲーム。
  • 事前予想 (prior assumption): 情報不完備ゲームでプレイヤーは、相手のタイプが不確実な状況において、相手のタイプを主観的に確率を見積もって予想する。この確率分布を事前予想という。
  • ハーサニー変換: 情報不完備ゲーム (game with incomplete information)と混同しがちな概念として、情報不完全ゲーム (games with imperfect information)があるが、これはプレイヤーの履歴について不完全な情報しか得られないゲーム。ハーサニーは、プレイヤーのタイプを定める偶然手番をゲームの初めに追加する事によって、情報不完備ゲームを情報完備な不完全情報ゲームに変換できることを示した。これをハーサニー変換という。
  • ベイジアン・ゲーム (Bayesian game): 情報不完備ゲームのモデルはベイジアン仮説を採用するので、ベイジアンゲームという。
  • ベイジアン均衡点 (Bayesian equilibrium): ベイジアンゲームにおける均衡点。ハーサニー変換により、ダイナミックなゲームでの戦略や均衡点の概念が同じ様に適用できる。
  • 完全ベイジアン均衡点 (Perfect Bayesian equilibrium): ベイジアン均衡点は、ダイナミックなゲームのナッシュ均衡点と同様に、信憑性のない脅しを含むという欠点を持つため、より強い均衡概念として完全ベイジアン均衡点がある。

2. プレイヤーの信念とベイズの定理

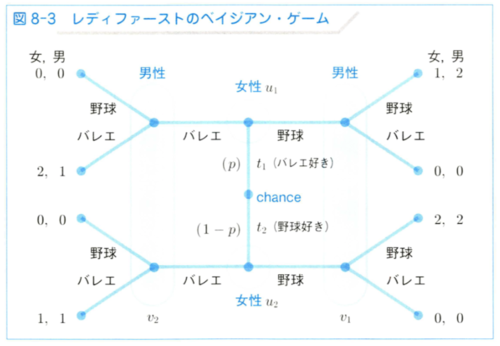
例: 情報不完備版レディファーストのゲーム

レディファーストのゲームにおいて、女性は男性の好みを知っているが、女性の好みは女性しか知らないとする。

＜バレエが好きな女性とのゲームの利得行列＞

男 \ 女 野球 バレエ
野球 2, 1 0, 0
バレエ 0, 0 1, 2

＜野球が好きな女性とのゲームの利得行列＞

男 \ 女 野球 バレエ
野球 2, 2 0, 0
バレエ 0, 0 1, 1

＜ゲームの木＞

＜行動戦略＞

  • 女性の行動戦略 b_1
    • 2つの情報集合 u_1、 u_2 でそれぞれ野球を選択する確率の組 b_1 = (b_{11}, b_{12}) で表される。
    • b_{11}: 情報集合 u_1 でバレエが好きな女性 (タイプ t_1) が野球を選択する確率 ( 0 \leq b_{11} \leq 1 )
    • b_{12}: 情報集合 u_2 で野球が好きな女性 (タイプ t_2) が野球を選択する確率 ( 0 \leq b_{12} \leq 1 )
    • 例えば b_1 = (0, 1) は、バレエ好きな女性がバレエを選び、野球好きな女性が野球を選ぶ行動戦略を表す。
  • 男性の行動戦略 b_2
    • 2つの情報集合 v_1、 v_2 でそれぞれ野球を選択する確率の組 b_2 = (b_{21}, b_{22}) で表される。
    • b_{21}: 女性が野球を選択したことを知った上で、情報集合 v_1 で男性が野球を選択する確率 ( 0 \leq b_{21} \leq 1 )
    • b_{22}: 女性がバレエを選択したことを知った上で、情報集合 v_2 で男性が野球を選択する確率 ( 0 \leq b_{22} \leq 1 )
    • 例えば b_2 = (1, 0) は、女性が野球を選択したことを知った上で野球を選び、女性がバレエを選択したことを知った上でバレエを選ぶ行動戦略を表す。

整合的な信念

  • 男性は女性のタイプを知らないが、女性の選択を知った上で、女性のタイプを予想することができる。女性のタイプを予想することは、言い換えると各情報集合の中で、どの手番にいるかを予想することである。
  • この様に、女性の選択を知った上で修正される男性の予想を事後予想、もしくは単に予想、信念 (belief) などと言う。
  • 男性の事後予想は、事前予想と女性の行動戦略から定まる。例えば、行動戦略 b_1 = (0, 1) が取られるとしよう。このとき女性がバレエを選択したことを知れば、合理的な男性であれば、女性はバレエ好きと予想できる。この様な、女性の行動戦略と矛盾しない男性の事後予想を、 b_1 と整合的であるという。
  • 一般に、女性の行動戦略 b_1 に対して、 b_1 と整合的な男性の信念 (事後予想) とは、ベイズの公式で定義される条件付き確率 p(t|v) = \frac{P (t \cap v)}{P (v)} である。
    • P (t \cap v): 女性がタイプ t であって、情報集合 v に手が進む確率
    • P (v: 情報集合 v に手が進む確率

女性が行動戦略 b1 = (0, 1) を選択する場合の整合的な信念

  • 女性の行動戦略 b_1 = (0, 1) は、バレエ好きな女性がバレエを選択し、野球好きな女性が野球を選択することを意味している。
  • 男性の事前予想は (p, 1 - p) である。
  • 情報集合 v_1 に手が進む確率は、女性が野球好きである事前予想確率と等しく P(v_1) = 1 - p である。女性がバレエ好き (タイプ t_1) で野球を選択する確率は P (t_1 \cap v_1) = 0 であり、女性が野球好き (タイプ t_2) で野球を選択する確率は P (t_2 \cap v_1) = 1 - p である。
  • 従って、男性の情報集合 v_1 に手が進むときに、女性のタイプが t = t_1, \: t_2 である条件付き確率 (整合的な信念) は、 p(t|v_1) = \frac{P(t \cap v_1)}{P(v_1)} = 0 ( t = t_1 の場合 ) or 1 ( t = t_2 の場合 ) である。
  • 同様に、男性の情報集合 v_2 に手が進むときに、女性のタイプが t = t_1, \: t_2 である条件付き確率 (整合的な信念) は、 p(t|v_2) = \frac{P(t \cap v_2)}{P(v_2)} = 1 ( t = t_1 の場合 ) or 0 ( t = t_2 の場合 ) である。
  • 男性の事前予想が女性の行動を踏まえて更新されることが分かる。

女性が一般の行動戦略 b1 = (b11, b12) を選択する場合の整合的な信念

  • b_{11} \gt 0、 b_{12} \gt 0 とする。
  • 男性の事前予想は (p, 1 - p) である。
  • この場合、情報集合 v_1 に手が進む確率は、女性が野球を選択する確率と等しいから、 P(v_1) = p b_{11} + (1 - p) b_{12} である。
  • 女性がタイプ t_1 で野球を選択する確率は P (t_1 \cap v_1) = p b_{11} であり、
  • 女性がタイプ t_2 で野球を選択する確率は P (t_2 \cap v_1) = (1 - p) b_{12} である。
  • 従って、男性の情報集合 v_1 に手が進むときに女性のタイプが t である条件付き確率 (整合的な信念) は、 p (t | v_1) = \frac{p b_{11}}{p b_{11} + (1 - p) b_{12}} ( t = t_1 の場合) or \frac{(1 - p) b_{12}}{p b_{11} + (1 - p) b_{12}} ( t = t_2 の場合) である。
  • 同様に、男性の情報集合 v_2 に手が進むときに女性のタイプが t である条件付き確率 (整合的な信念) は、 p (t | v_2) = \frac{p (1 - b_{11})}{p (1 - b_{11}) + (1 - p) (1 - b_{12})} ( t = t_1 の場合) or \frac{(1 - p) (1 - b_{12})}{p (1 - b_{11}) + (1 - p) (1 - b_{12})} ( t = t_2 の場合) である。
  • 男性の事前予想が女性の行動を踏まえて更新されることが分かる。

両方のタイプの女性が野球を選択する場合の整合的な信念

  • これは b_1 = (1, 1) ということ。
  • 男性の事前予想は (p, 1 - p) である。
  • どんなときでも野球を選択するので、必ず情報集合 v_1 に到達し、 P(v_1) = p + (1 - p) = 1 となる。
  • そして、 P(t_1 \cap v_1) = p で、 P(t_2 \cap v_1) = 1 - p である。
  • 従って、男性の情報集合 v_1 に手が進むときに女性のタイプが t である条件付き確率 (整合的な信念) は、 p (t | v_1) = p ( t = t_1 の場合) or 1 - p ( t = t2 の場合)
  • そして、情報集合 v_2 に手が進む確率 P(v_2) は 0 であり、分母が０になるため、ベイズの公式は使えない。この場合は、どんな信念も整合的と考える。
  • この場合は、女性の行動は何の情報も男性に与えず、男性の事前予想は更新されないことが分かる。

まとめ

以上をまとめると、プレイヤの行動戦略の組に対して、行動戦略と整合的なプレイヤーの信念は、次の性質を持つ。

性質8.1
情報集合が戦略によって到達可能なときは、予想はベイズの公式による条件付き確率と等しい。

性質8.2
情報集合が戦略によって到達可能でないときは、どんな予想も整合的とする。

3. 完全ベイジアン均衡点

展開形ゲームにおける部分ゲーム完全均衡点を、ベイジアンゲームや一般の不完全情報を持つ展開形ゲームに拡張した均衡概念が、完全ベイジアン均衡点である。

定義8.1
プレイヤーの行動戦略と信念の組が完全ベイジアン均衡点であるとは、全ての情報集合において次の２つの条件が成り立つことである。
(1) プレイヤーの信念は行動戦略と整合的である。
(2) プレイヤーの行動戦略は信念のもとで、他のプレイヤーの行動戦略に対して最適応答である。

以下で、完全ベイジアン均衡点と完全ではないベイジアン均衡点の例を確認する。

引き続き「情報不完備版レディファーストのゲーム」で説明する。

完全ベイジアン均衡点の例

  • 男性の情報集合 v_1 における最適戦略は、女性のタイプに関する信念に関わらず野球を選択することである。
  • 男性の情報集合 v_2 における最適戦略は、女性のタイプに関する信念に関わらずバレエを選択することである。
  • これを所与として女性の最適戦略を考えると、女性は自分の好みに応じて選択することが最適戦略であることが分かる。
  • まとめると、女性は自分の好みに応じて野球かバレエを選択する。男性は女性と同じ選択をする。男性の信念は、女性がバレエを選択するときは女性はバレエ好きなタイプであると予想し、女性が野球を選択するときは女性は野球好きなタイプであると予想することである。
    • 行動戦略 b_1 = (0, 1)
    • 行動戦略 b_2 = (1, 0)
    • 男性の信念は、下記の通りであり、これは女性の均衡戦略と整合的である。
      • p(t|v_1) = 0 ( t = t_1 の場合) or 1 ( t = t_2 の場合)
      • p(t|v_2) = 1 ( t = t_1 の場合) or 0 ( t = t_2 の場合)
  • この様に、行動からタイプを完全に判定できる場合の均衡点を、分離均衡 (separating equilibrium) という。

完全ではないベイジアン均衡点の例

  • 男性の戦略として、女性の選択とは無関係に常に野球を選択するものを考える。(こんな非合理な仮定を置けるなら何でもアリにならない？ → 仮定を置いていると言うよりも全ての戦略に関して検討した場合、当然こういう戦略も出てくるという話)
  • この時、女性の最適戦略は、自身の好みに関わらず、野球を選択することである。(意思決定の順番が逆になってるよね？女性が決めてから男が決めるというルールでは？ → 意思決定の順番は変わってない。後向き帰納法で検証しているだけ)
  • また、女性の行動戦略に対して、男性の行動戦略は最適応答であることが分かる。
  • まとめると、次の様なベイジアン均衡点が得られる。
    • 女性は自分の好みに関わらず野球を選択する。男性は女性の選択が何であっても野球を選択する。男性の信念は、女性が野球を選択するときは事前予想と同じであり、女性がバレエを選択するときはどんなものでもよい。
    • 情報集合 v_2 における男性の行動はいかなる信念のもとでも男性の最適戦略ではない (信憑性のない脅し) から、完全ベイジアン均衡点ではない。
  • この様に、行動からタイプを判定できない場合の均衡点を、一括均衡 (pooling equilibrium) という。

4. 逆選択とシグナリング

情報の非対称性による問題

情報の非対称性を放置しておくと、全体の利得が低下する。

例1: 中古車市場で、中古車の品質が不明だと、多くの人は安い価格でしか買わなくなり、そうすると高品質な車を中古車市場に売る人はいなくなり、ますます中古車市場に出回る車の品質は下がる。

例2: 保険の加入者には事故率の高い人と低い人がいるが、事故率の低い人は、事故率の高い人と同じ保険料を払う必要があり、不公平な状況にある。そのため、事故率の低い人の加入率は下がり、加入者に占める事故率の高い人の割合が増える。そうすると、保険料は上がり、ますます、事故率の高い人の割合が上がっていく。

この様に本来高品質の財が取引されるはずの市場で、逆に低品質の財が取引される現象を逆選択という。

逆選択を防ぐ有効な手段が、情報の保有者によるシグナリングだ。シグナリングとは、相手にシグナルを送って自分のタイプを知らせる行為をいう。

シグナリング・ゲーム

ベイジアンゲームを用いて、労働市場のシグナリングの分析を説明する。

ルール説明

  • ピザ店の経営者が労働者を1人雇用する。
  • 経営者の利得
    • 高い能力を持つ労働者 (タイプH) を採用すれば +1
    • 低い能力を持つ労働者 (タイプL) を採用すれば -1
    • 労働者を採用しないとき ±0
  • 経営者は労働者の能力を確実に知ることはできないが、これまでの採用実績からタイプ H とタイプ L の割合は 1 : 2 と推定している (事前予想)。
  • 経営者の期待利得は \frac{1}{3} \times 1 + \frac{2}{3} \times (-1) = -\frac{1}{3} であるから、経営者の最適行動は採用しないことである。その結果、能力の低い個人だけでなく、能力の高い個人も採用されないことになってしまい、社会にとって望ましくない。この時、資格を取得するなどのシグナルが有効に機能するかどうかを調べてみよう。
  • 個人の利得
    • タイプ H が資格を取得するコスト -2
    • タイプ L が資格を取得するコスト -5
    • 採用された場合 +3
    • 採用されなかった場合 ±0
  • ゲームの木
    • f:id:mas178:20200104002327p:plain
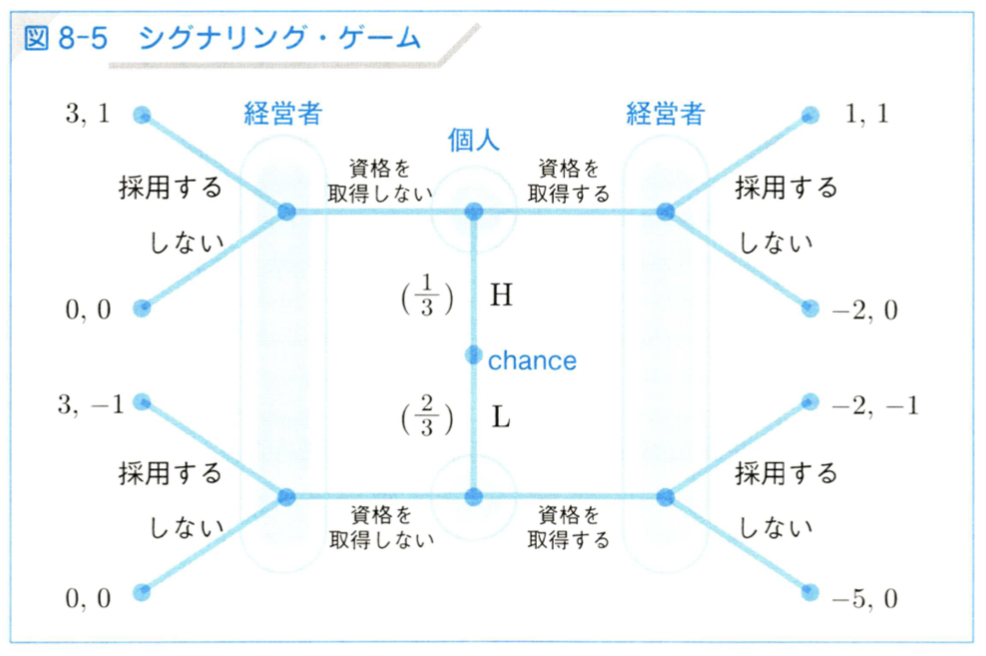
    • 左の数字が個人の利得で、右の数字が経営者の利得。
    • この様に最初に個人がシグナルを出すかどうかを選択するゲームを、シグナリング・ゲームという。

完全ベイジアン均衡点

  • タイプ L の最適行動は資格を取得しないことである。
    • タイプ L の個人が資格を取得すれば、利得はマイナス。
    • 資格を取得しなければ 0 または プラスの利得が得られる。
  • タイプ H が資格を取得する場合、次の行動戦略と信念の組は分離均衡の完全ベイジアン均衡点である。
    • 個人の行動戦略: タイプ H は資格を取得し、タイプ L は資格を取得しない。
    • 経営者の行動戦略: 資格取得した個人は採用し、資格取得していない個人は採用しない。
    • 経営者の信念: 個人が資格を取得するならばタイプ H と予想し、資格を取得しないならばタイプ L と予想する。
  • タイプ H の個人が資格を取得しない場合、次の行動戦略と信念の組は一括均衡の完全ベイジアン均衡点である。
    • 個人の行動戦略: どのタイプの個人も資格を取得しない。
    • 経営者の行動戦略: 経営者は個人が資格を取得したかどうかに関わらず雇用しない。
      • 左側の情報集合では信念は事前予想と同じ。よって経営者の最適行動は個人を採用しないことである。
      • 右側の情報集合では採用するときの経営者の期待利得は p \times 1 + (1 - p) \times (-1) = 2p - 1 であるから、 0 \leq p \lt \frac{1}{2} ならば経営者の最適行動は個人を採用しないこと、 \frac{1}{2} \leq p \leq 1 ならば経営者の最適行動は個人を採用することである。
    • 経営者の信念: 個人が資格を取得しないならば事前予想と同じであり、個人が資格を取得するならば、個人が高い能力を持つ確率 p を 0 \leq p \lt \frac{1}{2} と予想する。

分離均衡ではシグナルは有効であり、シグナルが有効であるためのキーポイントは、個人の能力によってシグナルのコストが異なることである。一括均衡ではシグナルが有効ではなく、非効率な結果となってしまう。

5. モラル・ハザード

モラル・ハザードとは

  • これまでは相手のタイプがわからない不完備情報ゲームを扱ってきた。この節では相手の行動が分からない不完全情報ゲームを扱う。
  • 相手の行動が分かれば選択できた最適な行動が取れず、自分だけでなく社会的にも非効率な結果が生じてしまうことをモラル・ハザードという。
  • もともとの意味は、保険に加入した人が、保険に加入したがゆえに不注意になり、それを考慮した保険会社が高い保険料を付け、保険に加入する人が少なくなってしまい、保険制度が十分に機能しなくなること。

プリンシパル=エージェント問題

概要

  • 労働者にできるだけ仕事をさせたい経営者と、同じ賃金ならできるだけ努力せずに済ませたい労働者がいる。労働者の努力の度合いは経営者からは見えず、努力に応じて賃金を支払うことができないため、労働者の努力水準は低くなり業績は悪化し、経営者と労働者の双方にとって望ましくない状況になる。これがモラル・ハザードの一例として知られるプリンシパル=エージェント問題。
  • 努力を見える化して、賃金を適正化すればこの状況は解決されそう。

ルール説明

  • 経営者 P はあるプロジェクトを実行するかどうかの選択に直面している。
    • プロジェクトが成功すれば 600万円 の利益が見込まれる。
    • プロジェクトが失敗すれば利益は 0 である。
  • プロジェクトの成功は、労働者 A の努力水準に依存している。
    • 努力水準が高い (H) 場合は、確率 0.8 で成功するが確率 0.2 で失敗する。
    • 努力水準が低い (L) 場合は、確率 1.0 で失敗する。
  • 労働者 A にとって高い努力水準のコストは 100万円 であり、低い努力水準のコストは 20万円 である。
  • 労働者の努力水準は経営者にとって観察可能ではないとする。
  • 経営者と労働者は共にリスク中立的である。

固定賃金契約を提示する場合

  • ゲームの木
    • f:id:mas178:20200104121034p:plain
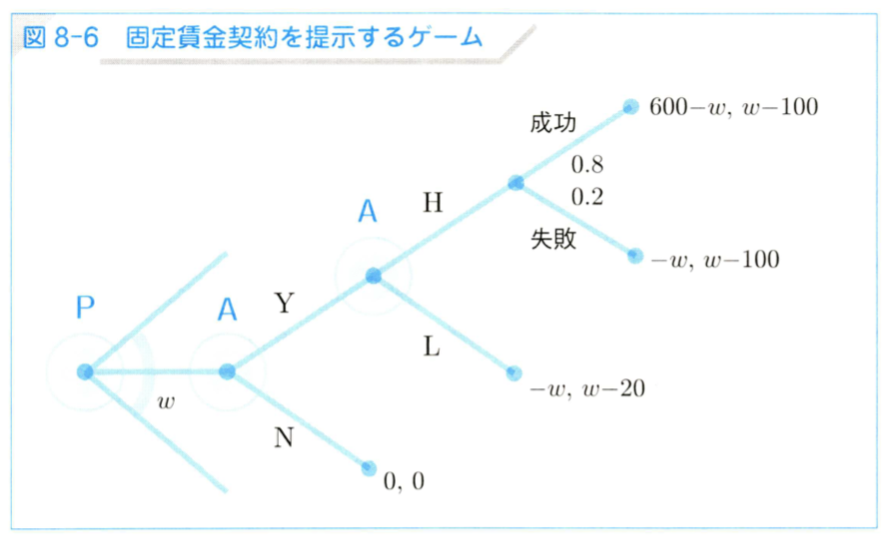
    • 左が経営者の利得で右が労働者の利得。
    • プロジェクトが成功するか失敗するかに依らず、努力水準 H の場合の労働者の利得は w - 100 だが、努力水準 L の場合の労働者の利得は w - 20 なので、労働者の最適行動は、L を選択すること。
    • これを前提に経営者が利得を最大化すると w = 0 となり、労働者は契約を受け入れず、プロジェクトは実行されず、両者の利得は 0。
    • もしプロジェクトを実行して労働者が高い努力水準を選択した場合、期待利得は 480 = 600 \times 0.8 で、労働者のコストは 100 なので、380 の総利得が生み出される。
  • この様に、プロジェクトの結果に関係のない固定賃金契約では労働者に高い努力水準を選択するインセンティブが与えられず、社会的に非効率な結果となってしまう。

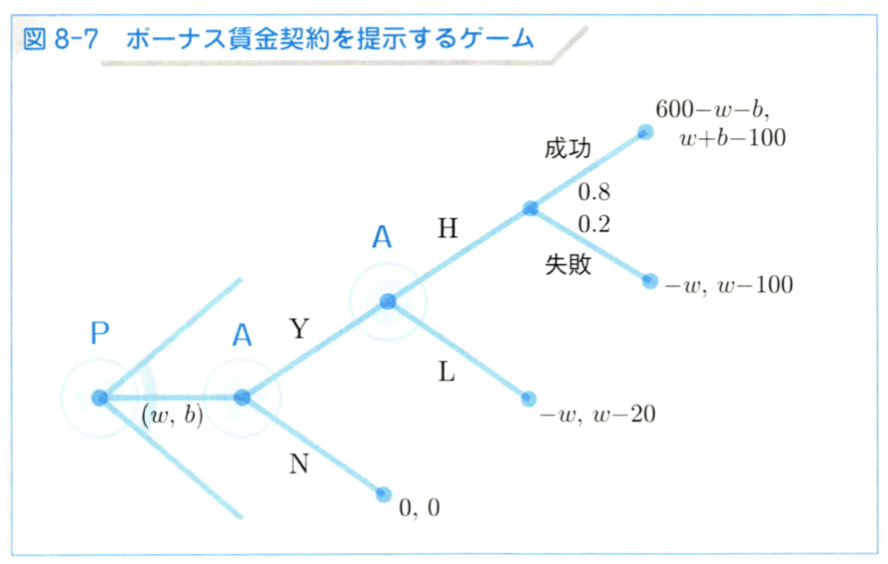
ボーナス賃金契約を提示する場合

  • ゲームの木
    • f:id:mas178:20200104122709p:plain
    • 固定賃金の木とのちがいは、プロジェクト成功時にボーナス b ( \geq 0) が支払われること。
    • 労働者が H を選択したときの期待利得は、 0.8 \times (w + b - 100) + 0.2 \times (w - 100) で、L を選択したときの期待利得は、 w - 20。両者が一致する条件をインセンティブ両立条件という。インセンティブ両立条件を解くと、 b \geq 100 となる。
    • 労働者が契約を受け入れるときの期待利得は、 0.8 \times (w + b - 100) + 0.2 \times (w - 100) で、受け入れないときの期待利得は 0。従って、労働者が契約を受け入れる条件 (参加条件) は、 w - 100 + 0.8b \geq 0 である。
    • 経営者の期待利得を最大にする (w, b) は、 b = 100 と w - 100 + 0.8b = 0 を解いて (20, 100) となる。
  • ボーナス賃金契約はプリンシパル=エージェント問題を解決し、社会的効率を高めていることが確認できた。
  • 現実の世界では、経営者が複数のプロジェクトにリスクを分散できるのに対して、労働者はリスクを分散できないので、労働者の方がリスク回避的であることが多く、ボーナスの比率を下げたほうが良い場合があることには留意が必要。

6. オークションの収入同値定理

オークションは、自分の評価額は知っているが他の参加者の評価額は知らないという情報不完備ゲームである。

ルール説明

  • 入札者1と入札者2がいる。
  • 各プレイヤーの商品の評価額は X_i とする。( i \in {1, 2}) ( X_i は 0 \leq X_i \leq 1 の独立な確率変数で、一様分布に従う。)
  • 入札者は自分の評価額は知っているが、他の入札者の評価額を知らない。
  • 入札者 i の戦略 b_i は、評価額のそれぞれの値 X_i = x に対して、入札額 b_i (x) を定めるものであり区間 [0, 1] の関数である。

ベイジアン均衡点を求める

第 1 価格入札ルール

  • 簡単の為に全ての入札者が同じ戦略 b_i(x) = kx ( 0 \leq k \leq 1 )を採用する均衡点を考える。この様な均衡点を対称均衡点という。
  • 入札者 2 が戦略 b_2 (x) = kx を採用する時の、入札者 1 最適な入札価格を計算する。
    • 入札者 2 の入札価格は高くても k である。
    • 入札者 1 の入札価格を p とおく。
    • 入札者 2 の入札額 kX_2 よりも p が高ければ入札に勝つ。
    • 入札者 1 が入札に勝つ確率 W(p) = P (X_2 \leq \frac{p}{k}) である。
    • 入札者 2 の評価額 X_2 は区間 [0, 1] 上に一様に分布するから、 W(p) = \frac{p}{k} である。
    • 入札者 1 の期待利得は f(p) = (\frac{p}{k}) \times (x - p) である。
    • これを p で微分して、入札者 1 の期待利得の最大値を求めると、 p^* = \frac{x}{2}, \: k = \frac{1}{2} となる。
  • よって、参加者が 2 名のとき、「評価額が x のとき、入札者 i は b_i(x) = \frac{x}{2} の価格を入札する」戦略の組は、第 1 価格ルールの元でベイジアン均衡点であることが分かる。
    • また、対称ベイジアン均衡点はこれ以外にないことが知られている。

第 2 価格入札ルール

第 2 価格入札ルールの元では、全ての入札者にとって評価額と等しい価格で入札することが弱支配戦略であることは、こちらで説明した。よって「全ての入札者 i が自分の評価額 b_i(x) = x を入札する」戦略の組がベイジアン均衡点である。

主催者の期待収入を求める

  • 主催者の期待収入は 2 人の入札者の期待支払金額の合計である。
  • どの価格ルールの元でも、評価額 x を持つ入札者 1 がオークションに勝つ確率は x である。
    • 入札者 1 がオークションに勝つ確率は、入札者 2 の評価額が x 以下である確率であり、
    • 入札者 2 の評価額は、区間 [0, 1] 上に一様に分布するから。

第 1 価格入札ルール

  • 入札者 1 の評価額が x の時に、入札者 1 が支払う期待金額は \frac{x}{2} \times x = \frac{x^2}{2} である。
  • 入札者 1 が主催者に支払う金額の期待値は \int_0^{1} \frac{x^2}{2} dx = \frac{1}{6} である。
    • 入札者 1 の評価額 x は区間 [0, \: 1] で一様に分布する。
    • 連続変数の期待値は積分を用いて計算する。
  • 対称均衡点では全ての入札者の支払う期待金額は等しいから、オークションの主催者の期待収入は \frac{1}{3}万円 である。

第 2 価格入札ルール

  • 評価額 x を持つ入札者 1 がオークションに勝つのは、相手の評価額 y が x 以下の場合であり、商品の価格は第 2 価格 y である。従って評価額 x を持つ入札者 1 の期待支払金額は \int_0^x y dy = \frac{x^2}{2} である。
  • 以降の計算は第 1 価格入札ルールと同じで、オークションの主催者の期待収入は \frac{1}{3}万円 となる。

この様に第 1 価格入札ルールの元でも、第 2 価格入札ルールの元でも、主催者が受け取る期待収入は同じになる。これは、入札者の数や入札者の評価額の確率分布に関わらず、一般的に成り立つことが知られている。

定理8.1 オークションの収入同値定理
入札者がリスク中立的であり、入札者の評価額が独立な同一分布に従う時、売り手の第 1 価格封印入札での期待収入と第 2 価格封印入札での期待収入は等しい。